Lia somou a pontuação que atingiu na realização de $ 3 $ testes.

O resultado dessa adição é
O desenho a seguir representa a parte do muro da escola que foi pintado.

A fração que pode representar a parte pintada é
O quadro em que $ 0,6 $ das bolas estão pintadas é:
A representação decimal da fração $ 1/2 $ é:
José desenhou apenas uma das figuras abaixo.
Considerando o lado de cada quadradinho como unidade de medida, o contorno de sua figura mede $ 22 $.
A figura que José desenhou é:
Certo automóvel consome, em média, $ 10 $ litros de combustível para percorrer $ 100\ km $. Mantendo essa média, a quantidade de litros de combustível que será necessária para que esse automóvel percorra $ 250\ km $ é
O resultado correto de $ (– 48) : (– 6) $ é:
As médias bimestrais de Matemática da turma do professor Fernando estão representadas na tabela a seguir.
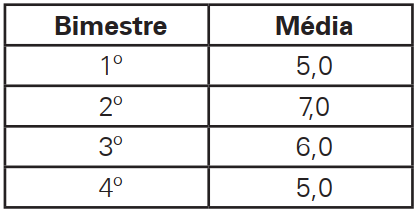
O gráfico que representa a situação descrita na tabela é:
Priscila possui $ R\$\ 5,00 $ e deseja fazer um lanche que incluirá um salgado e uma bebida. Observe a tabela a seguir com o preço de alguns produtos

Sabendo-se que Priscila precisa reservar $ R\$\ 2,30 $ para a passagem de ônibus, ela poderá pagar seu lanche se escolher
No sistema de coordenadas a seguir, o ponto $ A $ está localizado nas coordenadas $ (H,\ C) $.
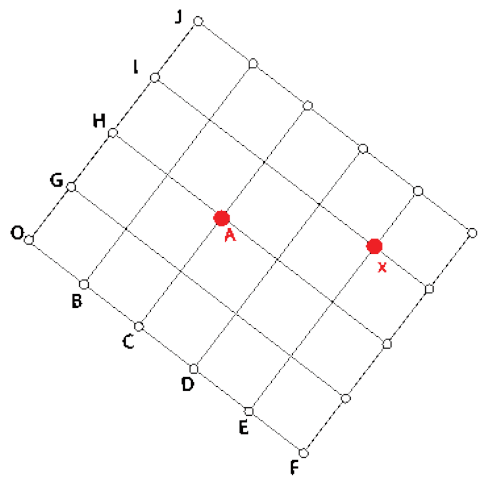
O ponto $ x $, por sua vez, está localizado nas coordenadas:
Das $ 100 $ pessoas que trabalharam durante $ 15 $ anos em contato com certa substância tóxica, $ 40 $ contraíram certa doença degenerativa. Dessas, $ 25\% $ vieram a falecer. Quantas pessoas vieram a falecer em razão dessa doença?
A tabela a seguir mostra o resumo de quatro pesquisas de opinião antes das eleições.

O resultado mais favorável ao candidato $ A $ foi o resultado da:
O resultado de 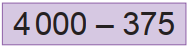 é:
é:
Durante uma semana, os alunos de uma escola fizeram uma campanha para arrecadar livros. A quantidade de livros arrecadados durante a campanha está indicada na tabela abaixo:
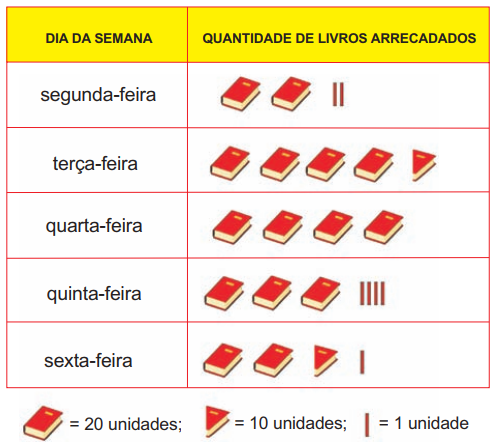
A quantidade total de livros arrecadados é igual a:
O número formado por sete unidades de milhar mais três unidades é
Calcule o saldo atual em reais $ (R\$) $ da conta bancária de Julia após as movimentações indicadas abaixo.
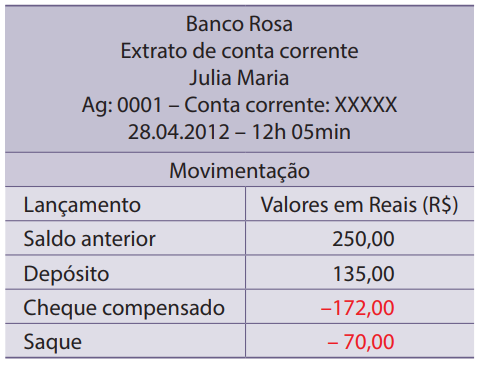
Calculando $ (–2)\ ×\ (–1)\ ×\ (–5) $ obtemos
A figura ilustra as posições das carteiras em uma sala de aula.
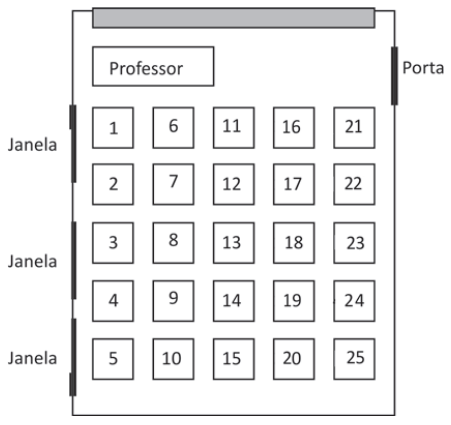
Gabriel está sentado à distância de uma carteira da janela e de duas carteiras da mesa do professor. Gabriel está sentado na carteira de número
Sobre uma circunferência de centro $ A $, dispõem-se os pontos $ B,\ C,\ D $ e $ E $.
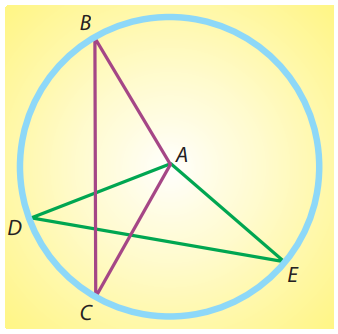
É correto afirmar que o segmento
Numa pesquisa realizada num condomínio, $ 35\% $ dos moradores apresentavam-se insatisfeitos com a administração do síndico.
A porcentagem de pessoas insatisfeitas equivale à fração
Dona Maria tem uma toalha de mesa com a forma de um pentágono regular, de lado $ 50\ cm $, e resolveu renová-la, aplicando uma faixa de renda em todo o seu contorno. Se um metro linear dessa renda custou $ R\$\ 11,50 $, então Dona Maria gastou com essa customização da toalha a quantia de
Observe a reta métrica a seguir

Os pontos $ A $, $ B $, $ C $ e $ D $ marcados na reta numérica representam os números
Paula mora em Sorocaba, na região indicada pela letra $ P $, e sua amiga Mara mora em Marília, na região indicada pela letra $ M $, conforme mostra o mapa
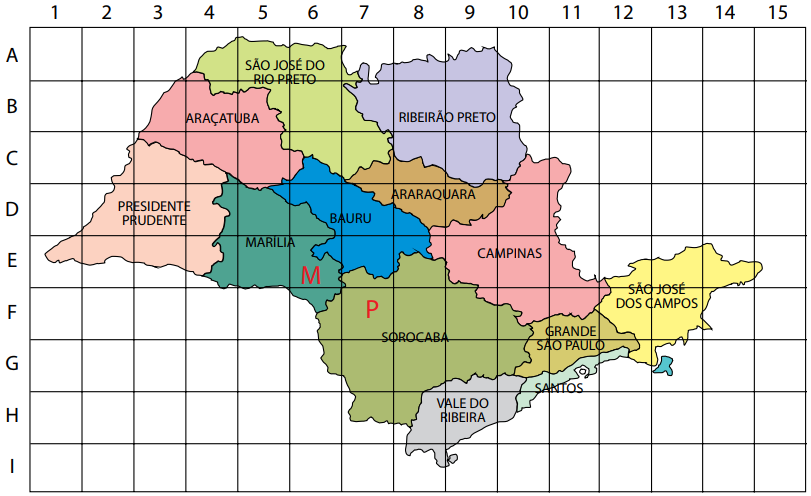
A localização das residências de Paula e Ana pode ser dada, respectivamente por,
Um vaso na forma de prisma de base quadrada tem $ 5\ dm^3 $ de capacidade.

Se colocarmos água até a metade da sua altura, teremos um volume de água de
A fração equivalente a $ \frac{2}{5} $ é
Estou palnejando uma viagem de automóvel. O consumo do veículo é de $ 10\ km/L $ e o preço do combustível é de $ R\$\ 2,00 $. Se a distância que irei percorrer é de $ 420\ km $ e o pedágio custa $ R\$\ 67,10 $, o valor que gastarei só para ir é
As variáveis $ x $ e $ n $ assumem valores conforme tabela abaixo.
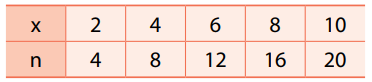
A relação $ x $ e $ n $ é dada pela expressão
Se colocados em ordem crescente os números decimais $ 0,05\ –\ 0,5\ –\ 0,003\ –\ 0,057\ –\ 0,35 $ têm-se
Carla precisa forrar um cômodo da casa que mede $ 5,30\ m $ de comprimento. A forração que ela tem mede $ 3,90\ m $ de comprimento e tem a mesma largura do cômodo. Para forrar o cômodo todo,
A Corrida Internacional de São Silvestre é a mais famosa corrida de rua no Brasil, realizada anualmente na cidade de São Paulo, no dia 31 de dezembro. A corrida possui um percurso de $ 15\ km $, o que é representado também por
Observe a figura 1 e assinale qual é o ângulo orientado que melhor descreve que a figura girou $ 180º $.

Na figura 1, tem-se um retângulo tomado como unidade de área. Na figura 2, está sombreada a quarta parte da unidade. Na figura 3, está sombreado um terço da unidade.
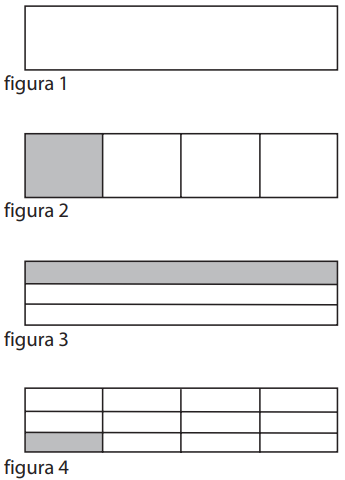
Na figura 4, a unidade está dividida em partes iguais e a região sombreada (uma dessas partes) corresponde a
Com as promoções que muitas companhias aéreas têm feito, fica cada vez mais fácil viajar de avião. Observe no gráfico abaixo o aumento do número de passageiros nos últimos anos.
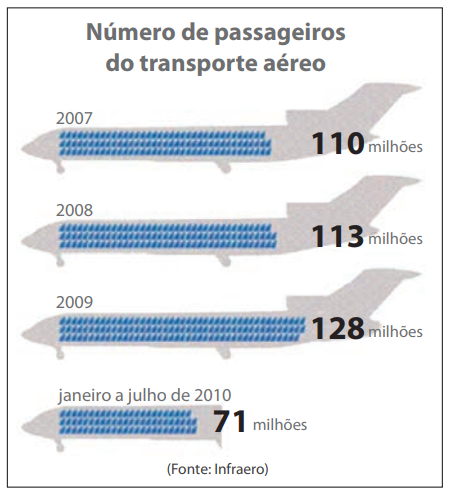
A tabela que melhor representa este gráfico é:
A decomposição $ 7 + 0,04 + 0,008 $ pode representar o número decimal
Para sustentar o telhado de um galpão cuja parede tem $ 3\ metros $ de altura, João colocou um conjunto de vigas, medindo, cada viga, $ 10\ metros $ de comprimento. Na figura, uma delas aparece apoiada nos pontos $ B $ e $ C $. A altura máxima do telhado, isto é, a distância $ AB $ é igual a $ 9\ metros $.
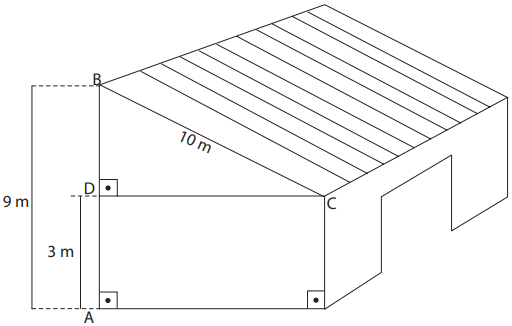
Pode-se concluir que a medida $ CD $ da parede do galpão mede, em metros,

