João e Maria colecionam selos e figurinhas e anotam a quantidade que têm no quadro a seguir:

O número de selos de João é igual a
Lia somou a pontuação que atingiu na realização de $ 3 $ testes.

O resultado dessa adição é
Um elevador tem capacidade para $ 350\ kg $. Quantas pessoas com peso igual a $ 70\ kg $ poderão entrar ao
mesmo tempo nesse elevador?
Observe o anúncio:

Hélio comprou esse teclado e pagou com uma nota de cem reais. Ele teve de troco?
Um funcionário de uma loja registrou em um gráfico como estava o estoque antes de a loja entrar em
liquidação.

De acordo com o gráfico, o total dos produtos no estoque é
Certo automóvel consome, em média, $ 10 $ litros de combustível para percorrer $ 100\ km $. Mantendo essa média, a quantidade de litros de combustível que será necessária para que esse automóvel percorra $ 250\ km $ é
O resultado correto de $ (– 48) : (– 6) $ é:
As médias bimestrais de Matemática da turma do professor Fernando estão representadas na tabela a seguir.
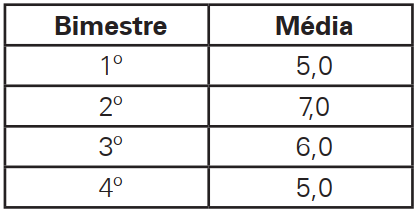
O gráfico que representa a situação descrita na tabela é:
Priscila possui $ R\$\ 5,00 $ e deseja fazer um lanche que incluirá um salgado e uma bebida. Observe a tabela a seguir com o preço de alguns produtos

Sabendo-se que Priscila precisa reservar $ R\$\ 2,30 $ para a passagem de ônibus, ela poderá pagar seu lanche se escolher
Das $ 100 $ pessoas que trabalharam durante $ 15 $ anos em contato com certa substância tóxica, $ 40 $ contraíram certa doença degenerativa. Dessas, $ 25\% $ vieram a falecer. Quantas pessoas vieram a falecer em razão dessa doença?
A tabela a seguir mostra o resumo de quatro pesquisas de opinião antes das eleições.

O resultado mais favorável ao candidato $ A $ foi o resultado da:
O número de bactérias de uma colônia reduz-se à metade a cada hora. Às dez horas da manhã havia $ 4000 $ bactérias na colônia. A quantidade de bactérias às duas horas da tarde é de
Mateus é técnico em computação e tem uma oficina de prestação de serviços. Para a reparação de
computadores com problemas, Mateus obedece à seguinte regra para cobrança dos serviços: $ C = 20x + 60 $,
onde $ C $ é o custo (em reais) e $ x $, o número de horas de trabalho no computador avariado.
Na semana passada, Mateus recebeu um computador com muitos problemas. Tantos que ele demorou $ 16 $ horas para consertá-lo.
Mateus recebeu por esse serviço, em reais,
O retângulo representado na figura tem $ 35\ m^2 $ de área.
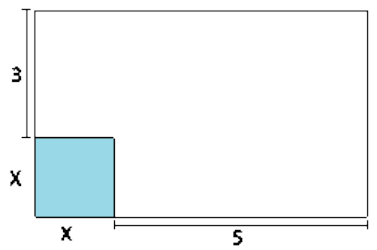
A área do quadrado sombreado é, em $ m^2 $, igual a
Na festa junina da escola de Pedro, havia uma barraca para o lançamento de setas ao alvo. Os alvos tinham os formatos mostrados nas figuras.
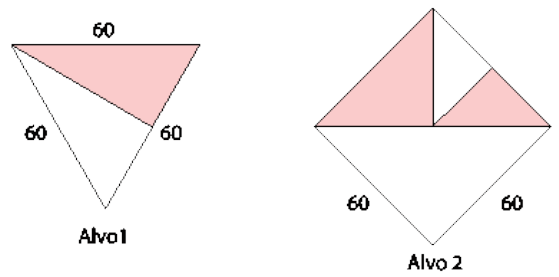
Assinale a alternativa que mostra a probabilidade de acertar na parte colorida de cada um dos alvos.
Um jovem avista o topo de uma torre segundo um ângulo de $ 45° $, conforme a ilustração.
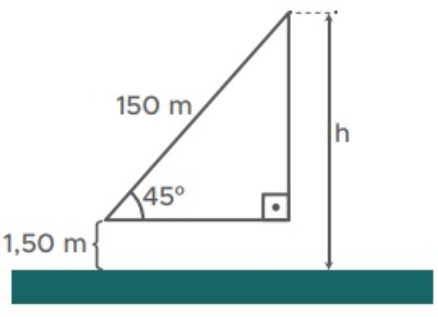
Sabe-se que a distância dos seus olhos ao topo da torre é $ 150\ m $ e, ainda, que a distância dos seus olhos ao solo é $ 1,50\ m $. A altura aproximada $ h $ da torre é
Considere: $ \sqrt{2} \cong 1,4 $
Os símbolos indicados na reta numérica abaixo correspondem a números naturais.

Sabendo-se que os pontos estão organizados em ordem crescente de $ 5 $ em $ 5 $ unidades, esse símbolos correspondem, respectivamente, aos números:
O número formado por sete unidades de milhar mais três unidades é
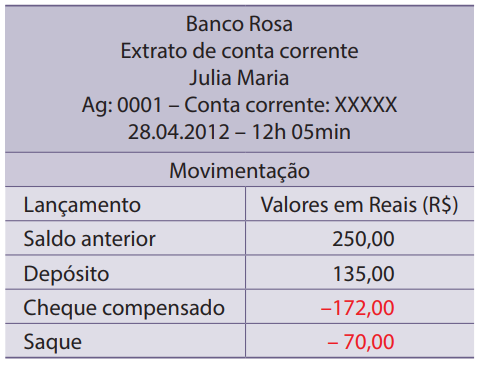
Calcule o saldo atual em reais $ (R\$) $ da conta bancária de Julia após as movimentações indicadas abaixo.
Calculando $ (–2)\ ×\ (–1)\ ×\ (–5) $ obtemos
A figura ilustra as posições das carteiras em uma sala de aula.
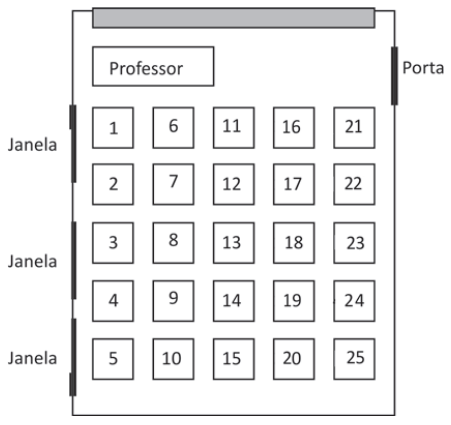
Gabriel está sentado à distância de uma carteira da janela e de duas carteiras da mesa do professor. Gabriel está sentado na carteira de número
Sobre uma circunferência de centro $ A $, dispõem-se os pontos $ B,\ C,\ D $ e $ E $.
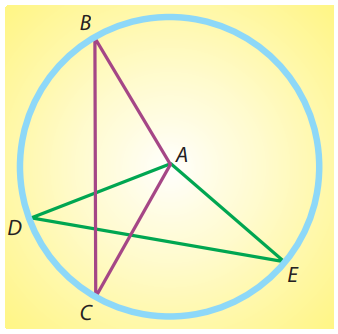
É correto afirmar que o segmento
Dona Maria tem uma toalha de mesa com a forma de um pentágono regular, de lado $ 50\ cm $, e resolveu renová-la, aplicando uma faixa de renda em todo o seu contorno. Se um metro linear dessa renda custou $ R\$\ 11,50 $, então Dona Maria gastou com essa customização da toalha a quantia de
Um remédio é administrado em pacientes em quantidades que são proporcionais às suas massas corporais. Se um paciente com $ 60 $ quilos precisa de $ 180 $ miligramas de remédio, a quantidade necessária para um paciente de $ 50 $ quilos é, em miligramas,
Considere um poliedro regular com $ 8 $ vértices, $ 6 $ faces, $ 12 $ arestas. Esse poliedro pode ser um(a)
Num ônibus intermunicipal, para estimar o lucro $ L $ em reais de uma viagem com a ocupação de $ x $ passageiros, adotou-se a expressão $ L(x) = (40 – x)(x – 10) $ para $ 10 < x < 40 $. O lucro máximo, em reais, que se pode obter nessa viagem é
A fração equivalente a $ \frac{2}{5} $ é
As variáveis $ x $ e $ n $ assumem valores conforme tabela abaixo.
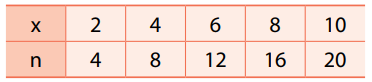
A relação $ x $ e $ n $ é dada pela expressão
Se colocados em ordem crescente os números decimais $ 0,05\ –\ 0,5\ –\ 0,003\ –\ 0,057\ –\ 0,35 $ têm-se
José precisava comprar ração e dar um banho em seu cão. Foi a uma "pet shop" e deparou-se com a seguinte promoção:

Qual o valor, em reais, do banho e da ração, respectivamente?
Os números de vértices, faces e arestas de um prisma de base pentagonal são, respectivamente,
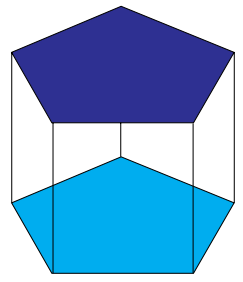
Renata foi à doceria comprar uma torta de limão. Cada pedaço da torta custa $ R\$\ 3,10 $, e a torta tem $ 8 $ pedaços.
Renata pagará pela torta toda
Uma loja de eletrodomésticos anunciou que os produtos estariam com $ 50\% $ de desconto.
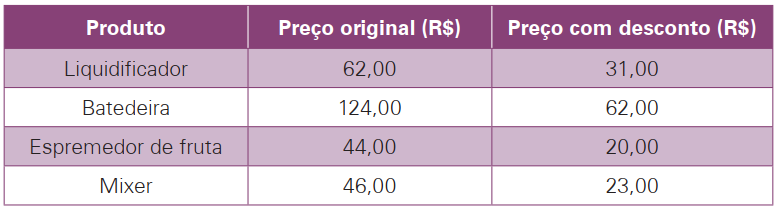
Josiane fez as contas e percebeu que haviam cometido um engano e um dos produtos anunciados não estava com o desconto. Qual é esse produto?
A figura a seguir representa a planta de uma casa.
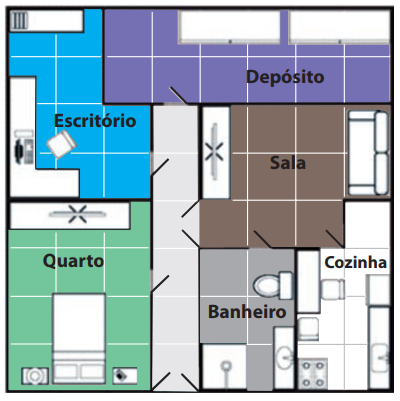
Sabendo-se que cada quadradinho tem a mesma medida, é correto afirmar que a área do quarto equivale à
Observe a figura 1 e assinale qual é o ângulo orientado que melhor descreve que a figura girou $ 180º $.

Na figura 1, tem-se um retângulo tomado como unidade de área. Na figura 2, está sombreada a quarta parte da unidade. Na figura 3, está sombreado um terço da unidade.
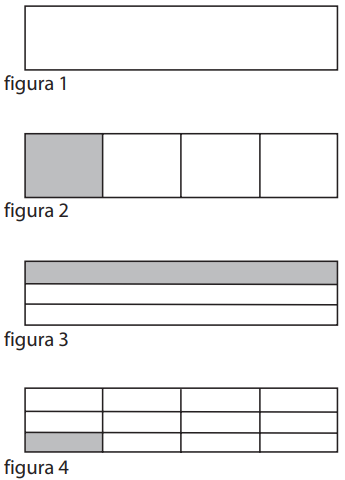
Na figura 4, a unidade está dividida em partes iguais e a região sombreada (uma dessas partes) corresponde a
Com as promoções que muitas companhias aéreas têm feito, fica cada vez mais fácil viajar de avião. Observe no gráfico abaixo o aumento do número de passageiros nos últimos anos.
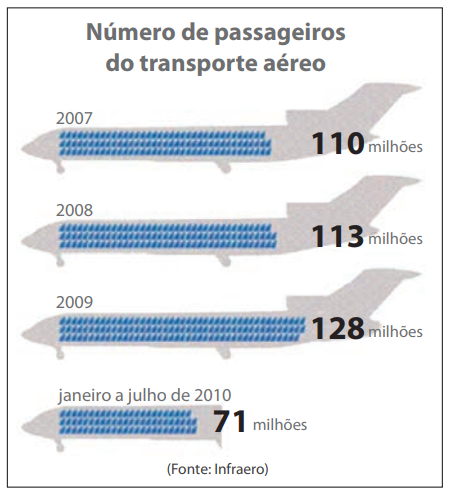
A tabela que melhor representa este gráfico é:
Observe os gráficos das funções $ f $ e $ g $.
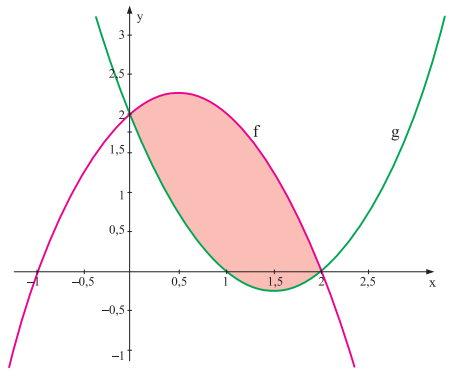
Essas funções têm uma raiz em comum, dada por $ x $ igual a
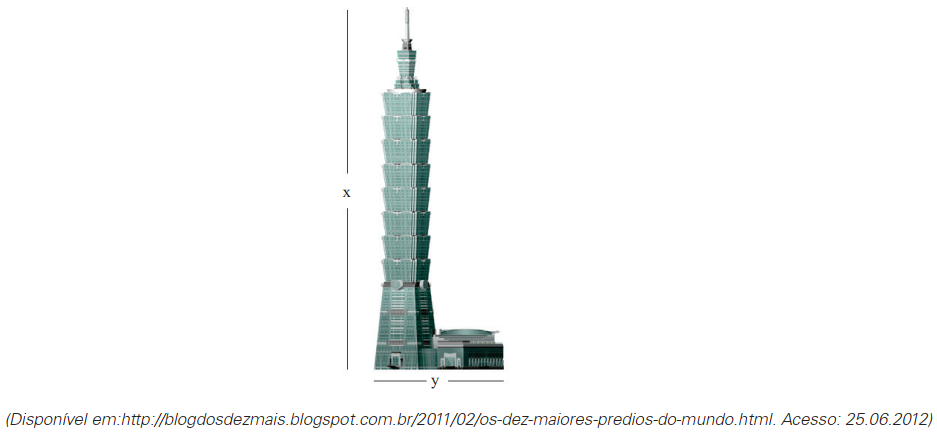
O edifício da foto abaixo foi construído em Taipei e é um dos dez mais altos do mundo. Sua altura real é de $ 509\ metros $. Se, na foto, a medida da altura $ x $ do prédio for de $ 14\ cm $ e a medida de $ y $ for de $ 5\ cm $, a medida real aproximada de $ y $ será de:
Uma indústria fabrica casquinhas para sorvetes na forma de cone, com $ 6\ cm $ de diâmetro na base e $ 12\ cm $ de altura, conforme a figura.
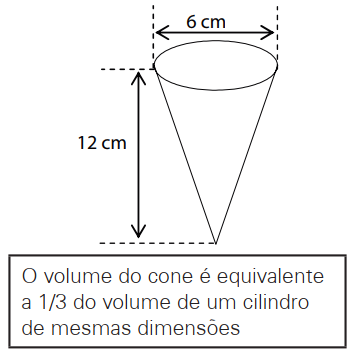
Se a altura desse cone for reduzida em $ 2\ cm $ e o diâmetro da base for mantido o mesmo, o novo volume, em relação ao volume inicial, será reduzido em:

